10. CIRCLES

MAX MARKS: – 18

TIME- 45MIN.        

1. A quadrilateral ABCD is drawn to circumscribe a circle , prove that  AB +CD =AD+BC

2. In Fig. 10.13, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠ AOB = 90°.

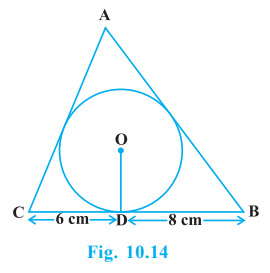
3.A triangle ABC is drawn to circumscribe a circle of radius 4cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8cm and 6cm respectively, find the sides of the AB and AC.

4.Prove that the length of a tangent drawn from an external point to a circle is equal.

5. Prove that the parallelogram circumscribing a circle is a rhombus.

6.The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.